elephant.kernels.EpanechnikovLikeKernel

class elephant.kernels.EpanechnikovLikeKernel(sigma, invert=False)

Class for Epanechnikov-like kernels.

\[\begin{split}K(t) = \left\{\begin{array}{ll} (3 /(4 d)) (1 - (t / d)^2), & |t| < d \\ 0, & |t| \geq d \end{array} \right.\end{split}\]

with \(d = \sqrt{5} \sigma\) being the half width of the kernel.

The Epanechnikov kernel under full consideration of its axioms has a half width of \(\sqrt{5}\). Ignoring one axiom also the respective kernel with half width = 1 can be called Epanechnikov kernel. However, arbitrary width of this type of kernel is here preferred to be called ‘Epanechnikov-like’ kernel.

The parameter invert has no effect on symmetric kernels.

Examples

from elephant import kernels
import quantities as pq
import numpy as np
import matplotlib.pyplot as plt

time_array = np.linspace(-3, 3, num=100) * pq.s
kernel = kernels.EpanechnikovLikeKernel(sigma=1*pq.s)
kernel_time = kernel(time_array)
plt.plot(time_array, kernel_time)
plt.title("EpanechnikovLikeKernel with sigma=1s")
plt.xlabel("time, s")
plt.ylabel("kernel, 1/s")
plt.show()

(Source code, png, hires.png, pdf)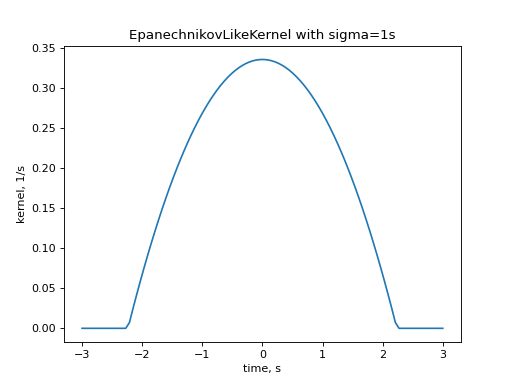

__init__(sigma, invert=False)

Methods

__init__(sigma[, invert])
boundary_enclosing_area_fraction(fraction)	Calculates the boundary \(b\) so that the integral from \(-b\) to \(b\) encloses a certain fraction of the integral over the complete kernel.
cdf(time)	Cumulative Distribution Function, CDF.
icdf(fraction)	Inverse Cumulative Distribution Function, ICDF, also known as a quantile.
is_symmetric()	True for symmetric kernels and False otherwise (asymmetric kernels).
median_index(times)	Estimates the index of the Median of the kernel.

Attributes

min_cutoff

Half width of the kernel.