Analysis of Sequences of Synchronous EvenTs (ASSET)¶
ASSET is a statistical method [1] for the detection of repeating sequences of synchronous spiking events in parallel spike trains. Given a list sts of spike trains, the analysis comprises the following steps:
Build the intersection matrix imat (optional) and the associated probability matrix pmat with the desired bin size:
>>> binsize = 5 * pq.ms >>> dt = 1 * pq.s >>> imat, xedges, yedges = intersection_matrix(sts, binsize, dt, norm=2) >>> pmat, xedges, yedges = probability_matrix_analytical( sts, binsize, dt)
Compute the joint probability matrix jmat, using a suitable filter:
>>> filter_shape = (5,2) # filter shape >>> nr_neigh = 5 # nr of largest neighbors >>> jmat = joint_probability_matrix(pmat, filter_shape, nr_neigh)
Create from pmat and jmat a masked version of the intersection matrix:
>>> alpha1 = 0.99 >>> alpha2 = 0.99999 >>> mask = mask_matrices([pmat, jmat], [alpha1, alpha2])
Cluster significant elements of imat into diagonal structures (“DSs”):
>>> epsilon = 10 >>> minsize = 2 >>> stretch = 5 >>> cmat = asset.cluster_matrix_entries(mask, epsilon, minsize, stretch)
Extract sequences of synchronous events associated to each worm
>>> extract_sse(sts, x_edges, y_edges, cmat)
References:
[1] Torre, Canova, Denker, Gerstein, Helias, Gruen (submitted)
-
elephant.asset.cluster_matrix_entries(mat, eps=10, min=2, stretch=5)[source]¶ Given a matrix mat, replaces its positive elements with integers representing different cluster ids. Each cluster comprises close-by elements.
In ASSET analysis, mat is a thresholded (“masked”) version of an intersection matrix imat, whose values are those of imat only if considered statistically significant, and zero otherwise.
A cluster is built by pooling elements according to their distance, via the DBSCAN algorithm (see sklearn.cluster.dbscan()). Elements form a neighbourhood if at least one of them has a distance not larger than eps from the others, and if they are at least min. Overlapping neighborhoods form a cluster.
- Clusters are assigned integers from 1 to the total number k of clusters
- Unclustered (“isolated”) positive elements of mat are assigned value -1
- Non-positive elements are assigned the value 0.
The distance between the positions of two positive elements in mat is given by an Euclidean metric which is stretched if the two positions are not aligned along the 45 degree direction (the main diagonal direction), as more, with maximal stretching along the anti-diagonal. Specifically, the Euclidean distance between positions (i1, j1) and (i2, j2) is stretched by a factor
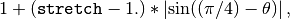
where
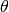 is the angle between the pixels and the 45deg
direction. The stretching factor thus varies between 1 and stretch.
is the angle between the pixels and the 45deg
direction. The stretching factor thus varies between 1 and stretch.Parameters: - mat : numpy.ndarray
a matrix whose elements with positive values are to be clustered.
- eps : float >=0, optional
the maximum distance for two elements in mat to be part of the same neighbourhood in the DBSCAN algorithm Default: 10
- min : int, optional
the minimum number of elements to form a neighbourhood. Default: 2
- stretch : float > 1, optional
the stretching factor of the euclidean metric for elements aligned along the 135 degree direction (anti-diagonal). The actual stretching increases from 1 to stretch as the direction of the two elements moves from the 45 to the 135 degree direction. Default: 5
Returns: - cmat : numpy.ndarray of integers
- a matrix with the same shape of mat, each of whose elements is either
- a positive int (cluster id) if the element is part of a cluster
- 0 if the corresponding element in mat was non-positive
- -1 if the element does not belong to any cluster
-
elephant.asset.extract_sse(spiketrains, x_edges, y_edges, cmat, ids=None)[source]¶ Given a list of spike trains, two arrays of bin edges and a clustered intersection matrix obtained from those spike trains via worms analysis using the specified edges, extracts the sequences of synchronous events (SSEs) corresponding to clustered elements in the cluster matrix.
Parameters: - spiketrains : list of neo.SpikeTrain
the spike trains analyzed for repeated sequences of synchronous events.
- x_edges : quantities.Quantity
the first array of time bins used to compute cmat
- y_edges : quantities.Quantity
the second array of time bins used to compute cmat. Musr have the same length as x_array
- cmat: numpy.ndarray
matrix of shape (n, n), where n is the length of x_edges and y_edges, representing the cluster matrix in worms analysis (see: cluster_matrix_entries())
- ids : list or None, optional
a list of spike train IDs. If provided, ids[i] is the identity of spiketrains[i]. If None, the IDs 0,1,…,n-1 are used Default: None
Returns: - sse : dict
a dictionary D of SSEs, where each SSE is a sub-dictionary Dk, k=1,…,K, where K is the max positive integer in cmat (the total number of clusters in cmat):
D = {1: D1, 2: D2, …, K: DK}
Each sub-dictionary Dk represents the k-th diagonal structure (i.e. the k-th cluster) in cmat, and is of the form
Dk = {(i1, j1): S1, (i2, j2): S2, …, (iL, jL): SL}.
The keys (i, j) represent the positions (time bin ids) of all elements in cmat that compose the SSE, i.e. that take value l (and therefore belong to the same cluster), and the values Sk are sets of neuron ids representing a repeated synchronous event (i.e. spiking at time bins i and j).
-
elephant.asset.intersection_matrix(spiketrains, binsize, dt, t_start_x=None, t_start_y=None, norm=None)[source]¶ Generates the intersection matrix from a list of spike trains.
Given a list of SpikeTrains, consider two binned versions of them differing for the starting time of the binning (t_start_x and t_start_y respectively; the two times can be identical). Then calculate the intersection matrix M of the two binned data, where M[i,j] is the overlap of bin i in the first binned data and bin j in the second binned data (i.e. the number of spike trains spiking both at bin i and at bin j). The matrix entries can be normalized to values between 0 and 1 via different normalizations (see below).
Parameters: - spiketrains : list of neo.SpikeTrains
list of SpikeTrains from which to compute the intersection matrix
- binsize : quantities.Quantity
size of the time bins used to define synchronous spikes in the given SpikeTrains.
- dt : quantities.Quantity
time span for which to consider the given SpikeTrains
- t_start_x : quantities.Quantity, optional
time start of the binning for the first axis of the intersection matrix, respectively. If None (default) the attribute t_start of the SpikeTrains is used (if the same for all spike trains). Default: None
- t_start_y : quantities.Quantity, optional
time start of the binning for the second axis of the intersection matrix
- norm : int, optional
type of normalization to be applied to each entry [i,j] of the intersection matrix. Given the sets s_i, s_j of neuron ids in the bins i, j respectively, the normalisation coefficient can be:
- norm = 0 or None: no normalisation (row counts)
- norm = 1: len(intersection(s_i, s_j))
- norm = 2: sqrt(len(s_1) * len(s_2))
- norm = 3: len(union(s_i, s_j))
Default: None
Returns: - imat : numpy.ndarray of floats
the intersection matrix of a list of spike trains. Has shape (n,n), where n is the number of bins time was discretized in.
- x_edges : numpy.ndarray
edges of the bins used for the horizontal axis of imat. If imat is a matrix of shape (n, n), x_edges has length n+1
- y_edges : numpy.ndarray
edges of the bins used for the vertical axis of imat. If imat is a matrix of shape (n, n), y_edges has length n+1
-
elephant.asset.joint_probability_matrix(pmat, filter_shape, nr_largest=None, alpha=0, pvmin=1e-05)[source]¶ Map a probability matrix pmat to a joint probability matrix jmat, where jmat[i, j] is the joint p-value of the largest neighbors of pmat[i, j].
The values of pmat are assumed to be uniformly distributed in the range [alpha, 1] (alpha=0 by default). Centered a rectangular kernel of shape filter_shape=(l, w) around each entry pmat[i, j], aligned along the diagonal where pmat[i, j] lies into, extracts the nr_largest highest values falling within the kernel and computes their joint p-value jmat[i, j] (see [1]).
Parameters: - pmat : ndarray
a square matrix of cumulative probability values between alpha and 1. The values are assumed to be uniformly distibuted in the said range
- filter_shape : tuple
a pair (l, w) of integers representing the kernel shape. The
- nr_largest : int, optional
the number of largest neighbors to collect for each entry in mat If None (default) the filter length l is used Default: 0
- alpha : float in [0, 1), optional
the left end of the range [alpha, 1] Default: 0
- pvmin : flaot in [0, 1), optional
minimum p-value for individual entries in pmat. Each pmat[i, j] is set to min(pmat[i, j], 1-pvmin) to avoid that a single highly significant value in pmat (extreme case: pmat[i, j] = 1) yield joint significance of itself and its neighbors. Default: 1e-5
Returns: - jmat : numpy.ndarray
joint probability matrix associated to pmat
References
[1] Torre et al (in prep) …
-
elephant.asset.mask_matrices(matrices, thresholds)[source]¶ Given a list of matrices and a list of thresholds, return a boolean matrix B (“mask”) such that B[i,j] is True if each input matrix in the list strictly exceeds the corresponding threshold at that position.
Parameters: - matrices : list of numpy.ndarrays
the matrices which are compared to the respective thresholds to build the mask. All matrices must have the same shape.
- thresholds : list of floats
list of thresholds
Returns: - mask : numpy.ndarray of bools
mask matrix with same shape of the input matrices.
-
elephant.asset.probability_matrix_analytical(spiketrains, binsize, dt, t_start_x=None, t_start_y=None, fir_rates='estimate', kernel_width=array(100.0) * ms, verbose=False)[source]¶ Given a list of spike trains, approximates the cumulative probability of each entry in their intersection matrix (see: intersection_matrix()).
The approximation is analytical and works under the assumptions that the input spike trains are independent and Poisson. It works as follows:
- Bin each spike train at the specified binsize: this yields a binary array of 1s (spike in bin) and 0s (no spike in bin) (clipping used)
- If required, estimate the rate profile of each spike train by convolving the binned array with a boxcar kernel of user-defined length
- For each neuron k and each pair of bins i and j, compute the probability p_ijk that neuron k fired in both bins i and j.
- Approximate the probability distribution of the intersection value at (i, j) by a Poisson distribution with mean parameter l = sum_k (p_ijk), justified by Le Cam’s approximation of a sum of independent Bernouilli random variables with a Poisson distribution.
Parameters: - spiketrains : list of neo.SpikeTrains
list of spike trains for whose intersection matrix to compute the p-values
- binsize : quantities.Quantity
width of the time bins used to compute the probability matrix
- dt : quantities.Quantity
time span for which to consider the given SpikeTrains
- t_start_x, t_start_y : quantities.Quantity, optional
time start of the binning for the first and second axes of the intersection matrix, respectively. If None (default) the attribute t_start of the SpikeTrains is used (if the same for all spike trains). Default: None
- fir_rates: list of neo.AnalogSignals or ‘estimate’, optional
if a list, fir_rate[i] is the firing rate of the spike train spiketrains[i]. If ‘estimate’, firing rates are estimated by simple boxcar kernel convolution, with specified kernel width (see below) Default: ‘estimate’
- kernel_width : quantities.Quantity, optional
total width of the kernel used to estimate the rate profiles when fir_rates=’estimate’. Default: 100 * pq.ms
- verbose : bool, optional
whether to print messages during the computation. Default: False
Returns: - pmat : numpy.ndarray
the cumulative probability matrix. pmat[i, j] represents the estimated probability of having an overlap between bins i and j STRICTLY LOWER THAN the observed overlap, under the null hypothesis of independence of the input spike trains.
- x_edges : numpy.ndarray
edges of the bins used for the horizontal axis of pmat. If pmat is a matrix of shape (n, n), x_edges has length n+1
- y_edges : numpy.ndarray
edges of the bins used for the vertical axis of pmat. If pmat is a matrix of shape (n, n), y_edges has length n+1
-
elephant.asset.probability_matrix_montecarlo(spiketrains, binsize, dt, t_start_x=None, t_start_y=None, surr_method='dither_spike_train', j=None, n_surr=100, verbose=False)[source]¶ - Given a list of parallel spike trains, estimate the cumulative probability
- of each entry in their intersection matrix (see: intersection_matrix())
by a Monte Carlo approach using surrogate data. Contrarily to the analytical version (see: probability_matrix_analytical()) the Monte Carlo one does not incorporate the assumptions of Poissonianity in the null hypothesis.
The method produces surrogate spike trains (using one of several methods at disposal, see below) and calculates their intersection matrix M. For each entry (i, j), the intersection cdf P[i, j] is then given by:
P[i, j] = #(spike_train_surrogates such that M[i, j] < I[i, j]) / #(spike_train_surrogates)
If P[i, j] is large (close to 1), I[i, j] is statistically significant: the probability to observe an overlap equal to or larger then I[i, j] under the null hypothesis is 1-P[i, j], very small.
Parameters: - sts : list of neo.SpikeTrains
list of spike trains for which to compute the probability matrix
- binsize : quantities.Quantity
width of the time bins used to compute the probability matrix
- dt : quantities.Quantity
time span for which to consider the given SpikeTrains
- t_start_x, t_start_y : quantities.Quantity, optional
time start of the binning for the first and second axes of the intersection matrix, respectively. If None (default) the attribute t_start of the SpikeTrains is used (if the same for all spike trains). Default: None
- surr_method : str, optional
the method to use to generate surrogate spike trains. Can be one of:
- ‘dither_spike_train’: see spike_train_surrogates.train_shifting() [dt needed]
- ‘spike_dithering’: see spike_train_surrogates.spike_dithering() [dt needed]
- ‘spike_jittering’: see spike_train_surrogates.spike_jittering() [dt needed]
- ‘spike_time_rand’: see spike_train_surrogates.spike_time_rand()
- ‘isi_shuffling’: see spike_train_surrogates.isi_shuffling()
Default: ‘dither_spike_train’
- j : quantities.Quantity, optional
For methods shifting spike times randomly around their original time (spike dithering, train shifting) or replacing them randomly within a certain window (spike jittering), j represents the size of that shift / window. For other methods, j is ignored. Default: None
- n_surr : int, optional
number of spike_train_surrogates to generate for the bootstrap procedure. Default: 100
Returns: - pmat : ndarray
the cumulative probability matrix. pmat[i, j] represents the estimated probability of having an overlap between bins i and j STRICTLY LOWER than the observed overlap, under the null hypothesis of independence of the input spike trains.
See also
-
elephant.asset.sse_difference(sse1, sse2, difference='linkwise')[source]¶ Given two sequences of synchronous events (SSEs) sse1 and sse2, each consisting of a pool of pixel positions and associated synchronous events (see below), computes the difference between sse1 and sse2. The difference can be performed ‘pixelwise’ or ‘linkwise’:
- if ‘pixelwise’, it yields a new SSE which contains all (and only) the events in sse1 whose pixel position doesn’t match any pixel in sse2.
- if ‘linkwise’, for each pixel (i, j) in sse1 and corresponding synchronous event S1, if (i, j) is a pixel in sse2 corresponding to the event S2, it retains the set difference S1 - S2. If (i, j) is not a pixel in sse2, it retains the full set S1.
Note that in either case the difference is a non-symmetric operation: intersection(sse1, sse2) != intersection(sse2, sse1).
Both sse1 and sse2 must be provided as dictionaries of the type
{(i1, j1): S1, (i2, j2): S2, …, (iK, jK): SK},
where each i, j is an integer and each S is a set of neuron ids. (See also: extract_sse() that extracts SSEs from given spiketrains).
Parameters: - sse1, sse2 : each a dict
a dictionary of pixel positions (i, j) as keys, and sets S of synchronous events as values (see above).
- difference : str, optional
the type of difference to perform between sse1 and sse2. Either ‘pixelwise’ or ‘linkwise’ (see above). Default: ‘linkwise’.
Returns: - sse : dict
a new SSE (same structure as sse1 and sse2) which retains the difference between sse1 and sse2 (see above).
-
elephant.asset.sse_intersection(sse1, sse2, intersection='linkwise')[source]¶ Given two sequences of synchronous events (SSEs) sse1 and sse2, each consisting of a pool of positions (iK, jK) of matrix entries and associated synchronous events SK, finds the intersection among them. The intersection can be performed ‘pixelwise’ or ‘linkwise’.
- if ‘pixelwise’, it yields a new SSE which retains only events in sse1 whose pixel position matches a pixel position in sse2. This operation is not symmetric: intersection(sse1, sse2) != intersection(sse2, sse1).
- if ‘linkwise’, an additional step is performed where each retained synchronous event SK in sse1 is intersected with the corresponding event in sse2. This yields a symmetric operation: intersection(sse1, sse2) = intersection(sse2, sse1).
Both sse1 and sse2 must be provided as dictionaries of the type
{(i1, j1): S1, (i2, j2): S2, …, (iK, jK): SK},
where each i, j is an integer and each S is a set of neuron ids. (See also: extract_sse() that extracts SSEs from given spiketrains).
Parameters: - sse1, sse2 : each a dict
each is a dictionary of pixel positions (i, j) as keys, and sets S of synchronous events as values (see above).
- intersection : str, optional
the type of intersection to perform among the two SSEs. Either ‘pixelwise’ or ‘linkwise’ (see above). Default: ‘linkwise’.
Returns: - sse : dict
a new SSE (same structure as sse1 and sse2) which retains only the events of sse1 associated to keys present both in sse1 and sse2. If intersection = ‘linkwise’, such events are additionally intersected with the associated events in sse2 (see above).
-
elephant.asset.sse_isdisjoint(sse1, sse2)[source]¶ Given two sequences of synchronous events (SSEs) sse1 and sse2, each consisting of a pool of pixel positions and associated synchronous events (see below), determines whether sse1 and sse2 are disjoint. Two SSEs are disjoint if they don’t share pixels, or if the events associated to common pixels are disjoint.
Both sse1 and sse2 must be provided as dictionaries of the type
{(i1, j1): S1, (i2, j2): S2, …, (iK, jK): SK},
where each i, j is an integer and each S is a set of neuron ids. (See also: extract_sse() that extracts SSEs from given spiketrains).
Parameters: - sse1, sse2 : each a dictionary
a dictionary of pixel positions (i, j) as keys, and sets S of synchronous events as values (see above).
Returns: - is_disjoint : bool
returns True if sse1 is disjoint from sse2.
-
elephant.asset.sse_isequal(sse1, sse2)[source]¶ Given two sequences of synchronous events (SSEs) sse1 and sse2, each consisting of a pool of pixel positions and associated synchronous events (see below), determines whether sse1 is strictly contained in sse2. sse1 is strictly contained in sse2 if all its pixels are pixels of sse2, if its associated events are subsets of the corresponding events in sse2, and if sse2 contains events, or neuron ids in some event, which do not belong to sse1 (i.e. sse1 and sse2 are not identical)
Both sse1 and sse2 must be provided as dictionaries of the type
{(i1, j1): S1, (i2, j2): S2, …, (iK, jK): SK},
where each i, j is an integer and each S is a set of neuron ids. (See also: extract_sse() that extracts SSEs from given spiketrains).
Parameters: - sse1, sse2 : each a dict
a dictionary of pixel positions (i, j) as keys, and sets S of synchronous events as values (see above).
Returns: - is_equal : bool
returns True if sse1 is identical to sse2
-
elephant.asset.sse_issub(sse1, sse2)[source]¶ Given two sequences of synchronous events (SSEs) sse1 and sse2, each consisting of a pool of pixel positions and associated synchronous events (see below), determines whether sse1 is strictly contained in sse2. sse1 is strictly contained in sse2 if all its pixels are pixels of sse2, if its associated events are subsets of the corresponding events in sse2, and if sse2 contains non-empty events, or neuron ids in some event, which do not belong to sse1 (i.e. sse1 and sse2 are not identical)
- Both sse1 and sse2 must be provided as dictionaries of the type
- {(i1, j1): S1, (i2, j2): S2, …, (iK, jK): SK},
where each i, j is an integer and each S is a set of neuron ids. (See also: extract_sse() that extracts SSEs from given spiketrains).
Parameters: - sse1, sse2 : each a dict
a dictionary of pixel positions (i, j) as keys, and sets S of synchronous events as values (see above).
Returns: - is_sub : bool
returns True if sse1 is a subset of sse2
-
elephant.asset.sse_issuper(sse1, sse2)[source]¶ Given two sequences of synchronous events (SSEs) sse1 and sse2, each consisting of a pool of pixel positions and associated synchronous events (see below), determines whether sse1 strictly contains sse2. sse1 strictly contains sse2 if it contains all pixels of sse2, if all associated events in sse1 contain those in sse2, and if sse1 additionally contains other pixels / events not contained in sse2.
- Both sse1 and sse2 must be provided as dictionaries of the type
- {(i1, j1): S1, (i2, j2): S2, …, (iK, jK): SK},
where each i, j is an integer and each S is a set of neuron ids. (See also: extract_sse() that extracts SSEs from given spiketrains).
Note: sse_issuper(sse1, sse2) is identical to sse_issub(sse2, sse1).
Parameters: - sse1, sse2 : each a dict
a dictionary of pixel positions (i, j) as keys, and sets S of synchronous events as values (see above).
Returns: - is_super : bool
returns True if sse1 strictly contains sse2.
-
elephant.asset.sse_overlap(sse1, sse2)[source]¶ Given two sequences of synchronous events (SSEs) sse1 and sse2, each consisting of a pool of pixel positions and associated synchronous events (see below), determines whether sse1 strictly contains sse2. sse1 strictly contains sse2 if it contains all pixels of sse2, if all associated events in sse1 contain those in sse2, and if sse1 additionally contains other pixels / events not contained in sse2.
- Both sse1 and sse2 must be provided as dictionaries of the type
- {(i1, j1): S1, (i2, j2): S2, …, (iK, jK): SK},
where each i, j is an integer and each S is a set of neuron ids. (See also: extract_sse() that extracts SSEs from given spiketrains).
Note: sse_issuper(sse1, sse2) is identical to sse_issub(sse2, sse1).
Parameters: - sse1, sse2 : each a dict
a dictionary of pixel positions (i, j) as keys, and sets S of synchronous events as values (see above).
Returns: - is_super : bool
returns True if sse1 strictly contains sse2.
