signal_processing - Signal processing¶
Basic processing procedures for analog signals (e.g., performing a z-score of a signal, or filtering a signal).
-
elephant.signal_processing.butter(signal, highpass_freq=None, lowpass_freq=None, order=4, filter_function='filtfilt', fs=1.0, axis=-1)[source]¶ Butterworth filtering function for neo.AnalogSignal. Filter type is determined according to how values of highpass_freq and lowpass_freq are given (see Parameters section for details).
Parameters: - signal : AnalogSignal or Quantity array or NumPy ndarray
Time series data to be filtered. When given as Quantity array or NumPy ndarray, the sampling frequency should be given through the keyword argument fs.
- highpass_freq, lowpass_freq : Quantity or float
High-pass and low-pass cut-off frequencies, respectively. When given as float, the given value is taken as frequency in Hz. Filter type is determined depending on values of these arguments:
- highpass_freq only (lowpass_freq = None): highpass filter
- lowpass_freq only (highpass_freq = None): lowpass filter
- highpass_freq < lowpass_freq: bandpass filter
- highpass_freq > lowpass_freq: bandstop filter
- order : int
Order of Butterworth filter. Default is 4.
- filter_function : string
Filtering function to be used. Either ‘filtfilt’ (scipy.signal.filtfilt()) or ‘lfilter’ (scipy.signal.lfilter()). In most applications ‘filtfilt’ should be used, because it doesn’t bring about phase shift due to filtering. Default is ‘filtfilt’.
- fs : Quantity or float
The sampling frequency of the input time series. When given as float, its value is taken as frequency in Hz. When the input is given as neo AnalogSignal, its attribute is used to specify the sampling frequency and this parameter is ignored. Default is 1.0.
- axis : int
Axis along which filter is applied. Default is -1.
Returns: - filtered_signal : AnalogSignal or Quantity array or NumPy ndarray
Filtered input data. The shape and type is identical to those of the input.
-
elephant.signal_processing.cross_correlation_function(signal, ch_pairs, env=False, nlags=None)[source]¶ Computes unbiased estimator of the cross-correlation function.
Calculates the unbiased estimator of the cross-correlation function [1]
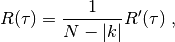
where
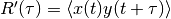 in a pairwise
manner, i.e. signal[ch_pairs[0,0]] vs signal2[ch_pairs[0,1]],
signal[ch_pairs[1,0]] vs signal2[ch_pairs[1,1]], and so on. The
cross-correlation function is obtained by scipy.signal.fftconvolve.
Time series in signal are zscored beforehand. Alternatively returns the
Hilbert envelope of
in a pairwise
manner, i.e. signal[ch_pairs[0,0]] vs signal2[ch_pairs[0,1]],
signal[ch_pairs[1,0]] vs signal2[ch_pairs[1,1]], and so on. The
cross-correlation function is obtained by scipy.signal.fftconvolve.
Time series in signal are zscored beforehand. Alternatively returns the
Hilbert envelope of 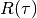 , which is useful to determine the
correlation length of oscillatory signals.
, which is useful to determine the
correlation length of oscillatory signals.Parameters: - signal : neo.AnalogSignal (nt x nch)
Signal with nt number of samples that contains nch LFP channels
- ch_pairs : list (or array with shape (n,2))
list with n channel pairs for which to compute cross-correlation, each element of list must contain 2 channel indices
- env : bool
Return Hilbert envelope of cross-correlation function Default: False
- nlags : int
Defines number of lags for cross-correlation function. Float will be rounded to nearest integer. Number of samples of output is 2*nlags+1. If None, number of samples of output is equal to number of samples of input signal, namely nt Default: None
Returns: - cross_corr : neo.AnalogSgnal (2*nlag+1 x n)
Pairwise cross-correlation functions for channel pairs given by ch_pairs. If env=True, the output is the Hilbert envelope of the pairwise cross-correlation function. This is helpful to compute the correlation length for oscillating cross-correlation functions
Raises: - ValueError
If the input signal is not a neo.AnalogSignal.
- ValueError
If ch_pairs is not a list of channel pair indices with shape (n,2).
- KeyError
If keyword env is not a boolean.
- KeyError
If nlags is not an integer or float larger than 0.
References
[1] (1, 2) Hall & River (2009) “Spectral Analysis of Signals, Spectral Element Method in Structural Dynamics”, Eq. 2.2.3 Examples
>>> dt = 0.02 >>> N = 2018 >>> f = 0.5 >>> t = np.arange(N)*dt >>> x = np.zeros((N,2)) >>> x[:,0] = 0.2 * np.sin(2.*np.pi*f*t) >>> x[:,1] = 5.3 * np.cos(2.*np.pi*f*t) >>> # Generate neo.AnalogSignals from x >>> signal = neo.AnalogSignal(x, units='mV', t_start=0.*pq.ms, >>> sampling_rate=1/dt*pq.Hz, dtype=float) >>> rho = elephant.signal_processing.cross_correlation_function( >>> signal, [0,1], nlags=150) >>> env = elephant.signal_processing.cross_correlation_function( >>> signal, [0,1], nlags=150, env=True) >>> plt.plot(rho.times, rho) >>> plt.plot(env.times, env) # should be equal to one >>> plt.show()
-
elephant.signal_processing.hilbert(signal, N='nextpow')[source]¶ Apply a Hilbert transform to an AnalogSignal object in order to obtain its (complex) analytic signal.
The time series of the instantaneous angle and amplitude can be obtained as the angle (np.angle) and absolute value (np.abs) of the complex analytic signal, respectively.
By default, the function will zero-pad the signal to a length corresponding to the next higher power of 2. This will provide higher computational efficiency at the expense of memory. In addition, this circumvents a situation where for some specific choices of the length of the input, scipy.signal.hilbert() will not terminate.
Parameters: - signal : neo.AnalogSignal
Signal(s) to transform
- N : string or int
- Defines whether the signal is zero-padded.
‘none’: no padding ‘nextpow’: zero-pad to the next length that is a power of 2 int: directly specify the length to zero-pad to (indicates the
number of Fourier components, see parameter N of scipy.signal.hilbert()).
Default: ‘nextpow’.
Returns: - neo.AnalogSignal
Contains the complex analytic signal(s) corresponding to the input signals. The unit of the analytic signal is dimensionless.
-
elephant.signal_processing.wavelet_transform(signal, freq, nco=6.0, fs=1.0, zero_padding=True)[source]¶ Compute the wavelet transform of a given signal with Morlet mother wavelet. The parametrization of the wavelet is based on [1].
Parameters: - signal : neo.AnalogSignal or array_like
Time series data to be wavelet-transformed. When multi-dimensional array_like is given, the time axis must be the last dimension of the array_like.
- freq : float or list of floats
Center frequency of the Morlet wavelet in Hz. Multiple center frequencies can be given as a list, in which case the function computes the wavelet transforms for all the given frequencies at once.
- nco : float (optional)
Size of the mother wavelet (approximate number of oscillation cycles within a wavelet; related to the wavelet number w as w ~ 2 pi nco / 6), as defined in [1]. A larger nco value leads to a higher frequency resolution and a lower temporal resolution, and vice versa. Typically used values are in a range of 3 - 8, but one should be cautious when using a value smaller than ~ 6, in which case the admissibility of the wavelet is not ensured (cf. [2]). Default value is 6.0.
- fs : float (optional)
Sampling rate of the input data in Hz. When signal is given as an AnalogSignal, the sampling frequency is taken from its attribute and this parameter is ignored. Default value is 1.0.
- zero_padding : bool (optional)
Specifies whether the data length is extended to the least power of 2 greater than the original length, by padding zeros to the tail, for speeding up the computation. In the case of True, the extended part is cut out from the final result before returned, so that the output has the same length as the input. Default is True.
Returns: - signal_wt: complex array
Wavelet transform of the input data. When freq was given as a list, the way how the wavelet transforms for different frequencies are returned depends on the input type. When the input was an AnalogSignal of shape (Nt, Nch), where Nt and Nch are the numbers of time points and channels, respectively, the returned array has a shape (Nt, Nch, Nf), where Nf = len(freq), such that the last dimension indexes the frequencies. When the input was an array_like of shape (a, b, …, c, Nt), the returned array has a shape (a, b, …, c, Nf, Nt), such that the second last dimension indexes the frequencies. To summarize, signal_wt.ndim = signal.ndim + 1, with the additional dimension in the last axis (for AnalogSignal input) or the second last axis (for array_like input) indexing the frequencies.
Raises: - ValueError
If freq (or one of the values in freq when it is a list) is greater than the half of fs, or nco is not positive.
References
- Le van Quyen et al. J Neurosci Meth 111:83-98 (2001)
- Farge, Annu Rev Fluid Mech 24:395-458 (1992)
-
elephant.signal_processing.zscore(signal, inplace=True)[source]¶ Apply a z-score operation to one or several AnalogSignal objects.
The z-score operation subtracts the mean
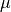 of the signal, and
divides by its standard deviation
of the signal, and
divides by its standard deviation 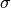 :
: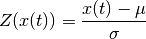
If an AnalogSignal containing multiple signals is provided, the z-transform is always calculated for each signal individually.
If a list of AnalogSignal objects is supplied, the mean and standard deviation are calculated across all objects of the list. Thus, all list elements are z-transformed by the same values of
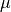 and
and
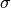 . For AnalogSignals, each signal of the array is
treated separately across list elements. Therefore, the number of signals
must be identical for each AnalogSignal of the list.
. For AnalogSignals, each signal of the array is
treated separately across list elements. Therefore, the number of signals
must be identical for each AnalogSignal of the list.Parameters: - signal : neo.AnalogSignal or list of neo.AnalogSignal
Signals for which to calculate the z-score.
- inplace : bool
If True, the contents of the input signal(s) is replaced by the z-transformed signal. Otherwise, a copy of the original AnalogSignal(s) is returned. Default: True
Returns: - neo.AnalogSignal or list of neo.AnalogSignal
The output format matches the input format: for each supplied AnalogSignal object a corresponding object is returned containing the z-transformed signal with the unit dimensionless.
Examples
>>> a = neo.AnalogSignal( ... np.array([1, 2, 3, 4, 5, 6]).reshape(-1,1)*mV, ... t_start=0*s, sampling_rate=1000*Hz)
>>> b = neo.AnalogSignal( ... np.transpose([[1, 2, 3, 4, 5, 6], [11, 12, 13, 14, 15, 16]])*mV, ... t_start=0*s, sampling_rate=1000*Hz)
>>> c = neo.AnalogSignal( ... np.transpose([[21, 22, 23, 24, 25, 26], [31, 32, 33, 34, 35, 36]])*mV, ... t_start=0*s, sampling_rate=1000*Hz)
>>> print zscore(a) [[-1.46385011] [-0.87831007] [-0.29277002] [ 0.29277002] [ 0.87831007] [ 1.46385011]] dimensionless
>>> print zscore(b) [[-1.46385011 -1.46385011] [-0.87831007 -0.87831007] [-0.29277002 -0.29277002] [ 0.29277002 0.29277002] [ 0.87831007 0.87831007] [ 1.46385011 1.46385011]] dimensionless
>>> print zscore([b,c]) [<AnalogSignal(array([[-1.11669108, -1.08361877], [-1.0672076 , -1.04878252], [-1.01772411, -1.01394628], [-0.96824063, -0.97911003], [-0.91875714, -0.94427378], [-0.86927366, -0.90943753]]) * dimensionless, [0.0 s, 0.006 s], sampling rate: 1000.0 Hz)>, <AnalogSignal(array([[ 0.78170952, 0.84779261], [ 0.86621866, 0.90728682], [ 0.9507278 , 0.96678104], [ 1.03523694, 1.02627526], [ 1.11974608, 1.08576948], [ 1.20425521, 1.1452637 ]]) * dimensionless, [0.0 s, 0.006 s], sampling rate: 1000.0 Hz)>]
