elephant.kernels.EpanechnikovLikeKernel¶
-
class
elephant.kernels.EpanechnikovLikeKernel(sigma, invert=False)[source]¶ Class for Epanechnikov-like kernels.
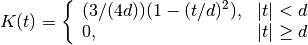
with
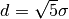 being the half width of the kernel.
being the half width of the kernel.The Epanechnikov kernel under full consideration of its axioms has a half width of
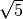 . Ignoring one axiom also the respective kernel
with half width = 1 can be called Epanechnikov kernel [1].
However, arbitrary width of this type of kernel is here preferred to be
called ‘Epanechnikov-like’ kernel.
. Ignoring one axiom also the respective kernel
with half width = 1 can be called Epanechnikov kernel [1].
However, arbitrary width of this type of kernel is here preferred to be
called ‘Epanechnikov-like’ kernel.The parameter invert has no effect on symmetric kernels.
References
[1] https://de.wikipedia.org/wiki/Epanechnikov-Kern Examples
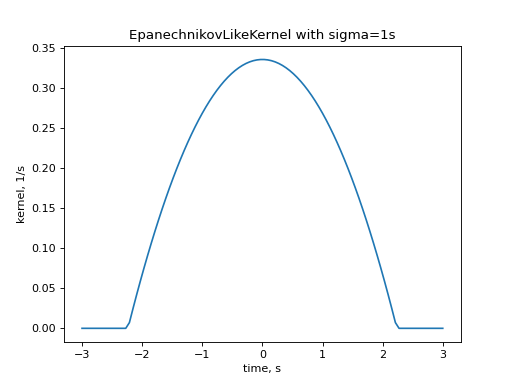
from elephant import kernels import quantities as pq import numpy as np import matplotlib.pyplot as plt time_array = np.linspace(-3, 3, num=100) * pq.s kernel = kernels.EpanechnikovLikeKernel(sigma=1*pq.s) kernel_time = kernel(time_array) plt.plot(time_array, kernel_time) plt.title("EpanechnikovLikeKernel with sigma=1s") plt.xlabel("time, s") plt.ylabel("kernel, 1/s") plt.show()
(Source code, png, hires.png, pdf)
Methods
__call__(times)Evaluates the kernel at all points in the array times. boundary_enclosing_area_fraction(fraction)Refer to Kernel.boundary_enclosing_area_fraction()for the documentation.cdf(time)Cumulative Distribution Function, CDF. icdf(fraction)Inverse Cumulative Distribution Function, ICDF, also known as a quantile. is_symmetric()True for symmetric kernels and False otherwise (asymmetric kernels). median_index(times)Estimates the index of the Median of the kernel. Attributes
min_cutoffHalf width of the kernel. -
boundary_enclosing_area_fraction(fraction)[source]¶ Refer to
Kernel.boundary_enclosing_area_fraction()for the documentation.Notes
For Epanechnikov-like kernels, integration of its density within the boundaries 0 and
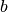 , and then solving for
, and then solving for 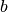 leads
to the problem of finding the roots of a polynomial of third order.
The implemented formulas are based on the solution of this problem
given in [1], where the following 3 solutions are given:
leads
to the problem of finding the roots of a polynomial of third order.
The implemented formulas are based on the solution of this problem
given in [1], where the following 3 solutions are given: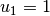 , solution on negative side;
, solution on negative side; , solution for larger
values than zero crossing of the density;
, solution for larger
values than zero crossing of the density;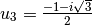 , solution for smaller
values than zero crossing of the density.
, solution for smaller
values than zero crossing of the density.
The solution
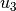 is the relevant one for the problem at hand,
since it involves only positive area contributions.
is the relevant one for the problem at hand,
since it involves only positive area contributions.References
[1] https://en.wikipedia.org/wiki/Cubic_function
-
cdf(time)[source]¶ Cumulative Distribution Function, CDF.
Parameters: - timepq.Quantity
The input time scalar.
Returns: - float
CDF at time.
-
icdf(fraction)[source]¶ Inverse Cumulative Distribution Function, ICDF, also known as a quantile.
Parameters: - fractionfloat
The fraction of CDF to compute the quantile from.
Returns: - pq.Quantity
The time scalar times such that CDF(t) = fraction.
-
is_symmetric()¶ True for symmetric kernels and False otherwise (asymmetric kernels).
A kernel is symmetric if its PDF is symmetric w.r.t. time:
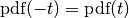
Returns: - bool
Whether the kernels is symmetric or not.
-
median_index(times)¶ Estimates the index of the Median of the kernel.
We define the Median index
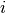 of a kernel as:
of a kernel as: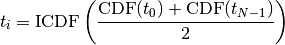
where
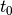 and
and 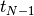 are the first and last entries of
the input array, CDF and ICDF stand for Cumulative Distribution
Function and its Inverse, respectively.
are the first and last entries of
the input array, CDF and ICDF stand for Cumulative Distribution
Function and its Inverse, respectively.This function is not mandatory for symmetrical kernels but it is required when asymmetrical kernels have to be aligned at their median.
Parameters: - timespq.Quantity
Vector with the interval on which the kernel is evaluated.
Returns: - int
Index of the estimated value of the kernel median.
Raises: - TypeError
If the input array is not a time pq.Quantity array.
- ValueError
If the input array is empty. If the input array is not sorted.
See also
Kernel.cdf- cumulative distribution function
Kernel.icdf- inverse cumulative distribution function
-
property
min_cutoff¶ Half width of the kernel.
Returns: - float
The returned value varies according to the kernel type.
-
