Signal processing¶
Basic processing procedures for analog signals (e.g., performing a z-score of a signal, or filtering a signal).
-
elephant.signal_processing.butter(signal, highpass_freq=None, lowpass_freq=None, order=4, filter_function='filtfilt', fs=1.0, axis=-1)[source]¶ Butterworth filtering function for neo.AnalogSignal. Filter type is determined according to how values of highpass_freq and lowpass_freq are given (see Parameters section for details).
Parameters: - signal : AnalogSignal or Quantity array or NumPy ndarray
Time series data to be filtered. When given as Quantity array or NumPy ndarray, the sampling frequency should be given through the keyword argument fs.
- highpass_freq, lowpass_freq : Quantity or float
High-pass and low-pass cut-off frequencies, respectively. When given as float, the given value is taken as frequency in Hz. Filter type is determined depending on values of these arguments:
- highpass_freq only (lowpass_freq = None): highpass filter
- lowpass_freq only (highpass_freq = None): lowpass filter
- highpass_freq < lowpass_freq: bandpass filter
- highpass_freq > lowpass_freq: bandstop filter
- order : int
Order of Butterworth filter. Default is 4.
- filter_function : string
Filtering function to be used. Either ‘filtfilt’ (scipy.signal.filtfilt()) or ‘lfilter’ (scipy.signal.lfilter()). In most applications ‘filtfilt’ should be used, because it doesn’t bring about phase shift due to filtering. Default is ‘filtfilt’.
- fs : Quantity or float
The sampling frequency of the input time series. When given as float, its value is taken as frequency in Hz. When the input is given as neo AnalogSignal, its attribute is used to specify the sampling frequency and this parameter is ignored. Default is 1.0.
- axis : int
Axis along which filter is applied. Default is -1.
Returns: - filtered_signal : AnalogSignal or Quantity array or NumPy ndarray
Filtered input data. The shape and type is identical to those of the input.
-
elephant.signal_processing.hilbert(signal, N='nextpow')[source]¶ Apply a Hilbert transform to an AnalogSignal object in order to obtain its (complex) analytic signal.
The time series of the instantaneous angle and amplitude can be obtained as the angle (np.angle) and absolute value (np.abs) of the complex analytic signal, respectively.
By default, the function will zero-pad the signal to a length corresponding to the next higher power of 2. This will provide higher computational efficiency at the expense of memory. In addition, this circumvents a situation where for some specific choices of the length of the input, scipy.signal.hilbert() will not terminate.
Parameters: - signal : neo.AnalogSignal
Signal(s) to transform
- N : string or int
- Defines whether the signal is zero-padded.
‘none’: no padding ‘nextpow’: zero-pad to the next length that is a power of 2 int: directly specify the length to zero-pad to (indicates the
number of Fourier components, see parameter N of scipy.signal.hilbert()).
Default: ‘nextpow’.
Returns: - neo.AnalogSignal
Contains the complex analytic signal(s) corresponding to the input signals. The unit of the analytic signal is dimensionless.
-
elephant.signal_processing.zscore(signal, inplace=True)[source]¶ Apply a z-score operation to one or several AnalogSignal objects.
The z-score operation subtracts the mean
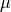 of the signal, and
divides by its standard deviation
of the signal, and
divides by its standard deviation  :
:
If an AnalogSignal containing multiple signals is provided, the z-transform is always calculated for each signal individually.
If a list of AnalogSignal objects is supplied, the mean and standard deviation are calculated across all objects of the list. Thus, all list elements are z-transformed by the same values of
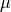 and
and
 . For AnalogSignals, each signal of the array is
treated separately across list elements. Therefore, the number of signals
must be identical for each AnalogSignal of the list.
. For AnalogSignals, each signal of the array is
treated separately across list elements. Therefore, the number of signals
must be identical for each AnalogSignal of the list.Parameters: - signal : neo.AnalogSignal or list of neo.AnalogSignal
Signals for which to calculate the z-score.
- inplace : bool
If True, the contents of the input signal(s) is replaced by the z-transformed signal. Otherwise, a copy of the original AnalogSignal(s) is returned. Default: True
Returns: - neo.AnalogSignal or list of neo.AnalogSignal
The output format matches the input format: for each supplied AnalogSignal object a corresponding object is returned containing the z-transformed signal with the unit dimensionless.
Examples
>>> a = neo.AnalogSignal( ... np.array([1, 2, 3, 4, 5, 6]).reshape(-1,1)*mV, ... t_start=0*s, sampling_rate=1000*Hz)
>>> b = neo.AnalogSignal( ... np.transpose([[1, 2, 3, 4, 5, 6], [11, 12, 13, 14, 15, 16]])*mV, ... t_start=0*s, sampling_rate=1000*Hz)
>>> c = neo.AnalogSignal( ... np.transpose([[21, 22, 23, 24, 25, 26], [31, 32, 33, 34, 35, 36]])*mV, ... t_start=0*s, sampling_rate=1000*Hz)
>>> print zscore(a) [[-1.46385011] [-0.87831007] [-0.29277002] [ 0.29277002] [ 0.87831007] [ 1.46385011]] dimensionless
>>> print zscore(b) [[-1.46385011 -1.46385011] [-0.87831007 -0.87831007] [-0.29277002 -0.29277002] [ 0.29277002 0.29277002] [ 0.87831007 0.87831007] [ 1.46385011 1.46385011]] dimensionless
>>> print zscore([b,c]) [<AnalogSignal(array([[-1.11669108, -1.08361877], [-1.0672076 , -1.04878252], [-1.01772411, -1.01394628], [-0.96824063, -0.97911003], [-0.91875714, -0.94427378], [-0.86927366, -0.90943753]]) * dimensionless, [0.0 s, 0.006 s], sampling rate: 1000.0 Hz)>, <AnalogSignal(array([[ 0.78170952, 0.84779261], [ 0.86621866, 0.90728682], [ 0.9507278 , 0.96678104], [ 1.03523694, 1.02627526], [ 1.11974608, 1.08576948], [ 1.20425521, 1.1452637 ]]) * dimensionless, [0.0 s, 0.006 s], sampling rate: 1000.0 Hz)>]
