elephant.kernels.EpanechnikovLikeKernel

class elephant.kernels.EpanechnikovLikeKernel(sigma, invert=False)[source]

Class for epanechnikov-like kernels.

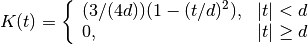
K(t) = \left\{\begin{array}{ll} (3 /(4 d)) (1 - (t / d)^2), & |t| < d \\ 0, & |t| \geq d \end{array} \right.

with 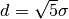d = \sqrt{5} \sigma being the half width of the kernel.

The Epanechnikov kernel under full consideration of its axioms has a half width of 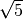\sqrt{5}. Ignoring one axiom also the respective kernel with half width = 1 can be called Epanechnikov kernel [Rc3a392fda6c4-1]. However, arbitrary width of this type of kernel is here preferred to be called ‘Epanechnikov-like’ kernel.

Besides the standard deviation sigma, for consistency of interfaces the parameter invert needed for asymmetric kernels also exists without having any effect in the case of symmetric kernels.

References

[Rc3a392fda6c4-1]https://de.wikipedia.org/wiki/Epanechnikov-Kern
Attributes:
min_cutofffloat

Half width of the kernel.
__call__(self, t)

Evaluates the kernel at all points in the array t.

Parameters:
tpq.Quantity

Vector with the interval on which the kernel is evaluated, not necessarily a time interval.
Returns:
pq.Quantity

Vector with the result of the kernel evaluations.
Raises:
TypeError

If t is not pq.Quantity.

If the dimensionality of t and sigma are different.
boundary_enclosing_area_fraction(self, fraction)[source]

Refer to Kernel.boundary_enclosing_area_fraction() for the documentation.

Notes

For Epanechnikov-like kernels, integration of its density within the boundaries 0 and 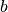b, and then solving for 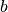b leads to the problem of finding the roots of a polynomial of third order. The implemented formulas are based on the solution of this problem given in [1], where the following 3 solutions are given:

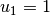  • u_1 = 1, solution on negative side;
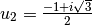  • u_2 = \frac{-1 + i\sqrt{3}}{2}, solution for larger values than zero crossing of the density;
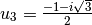  • u_3 = \frac{-1 - i\sqrt{3}}{2}, solution for smaller values than zero crossing of the density.

The solution 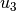u_3 is the relevant one for the problem at hand, since it involves only positive area contributions.

References

[1]https://en.wikipedia.org/wiki/Cubic_function
is_symmetric(self)

In the case of symmetric kernels, this method is overwritten in the class SymmetricKernel, where it returns True, hence leaving the here returned value False for the asymmetric kernels.

Returns:
bool

True in classes SymmetricKernel, RectangularKernel, TriangularKernel, EpanechnikovLikeKernel, GaussianKernel, and LaplacianKernel. False in classes Kernel, ExponentialKernel, and AlphaKernel.
property min_cutoff

Half width of the kernel.

Returns:
float

The returned value varies according to the kernel type.