Spike train correlation¶
This modules provides functions to calculate correlations between spike trains.
-
elephant.spike_train_correlation.corrcoef(binned_sts, binary=False, fast=True)[source]¶ Calculate the NxN matrix of pairwise Pearson’s correlation coefficients between all combinations of N binned spike trains.
For each pair of spike trains
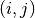 , the correlation coefficient
, the correlation coefficient
![C[i,j]](../_images/math/bf98d44b10da7feeb3ab48513f947f6939e208a9.png) is obtained by binning
is obtained by binning 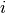 and
and 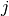 at the
desired bin size. Let
at the
desired bin size. Let 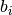 and
and  denote the binned spike
trains and
denote the binned spike
trains and 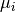 and
and 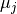 their respective means. Then
their respective means. Then![C[i,j] = <b_i-\mu_i, b_j-\mu_j> /
\sqrt{<b_i-\mu_i, b_i-\mu_i> \cdot <b_j-\mu_j, b_j-\mu_j>}](../_images/math/09c96cd3939401b9a6cde741c06d65e88db0698e.png)
where <., .> is the scalar product of two vectors.
For an input of N spike trains, an N x N matrix is returned. Each entry in the matrix is a real number ranging between -1 (perfectly anti-correlated spike trains) and +1 (perfectly correlated spike trains). However, if k-th spike train is empty, k-th row and k-th column of the returned matrix are set to np.nan.
If binary is True, the binned spike trains are clipped to 0 or 1 before computing the correlation coefficients, so that the binned vectors
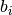 and
and  are binary.
are binary.Parameters: - binned_sts(N, ) elephant.conversion.BinnedSpikeTrain
A binned spike train containing the spike trains to be evaluated.
- binarybool, optional
If True, two spikes of a particular spike train falling in the same bin are counted as 1, resulting in binary binned vectors
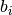 . If
False, the binned vectors
. If
False, the binned vectors 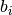 contain the spike counts per bin.
Default: False.
contain the spike counts per bin.
Default: False.- fastbool, optional
If fast=True and the sparsity of binned_sts is > 0.1, use np.corrcoef(). Otherwise, use memory efficient implementation. See Notes[2] Default: True.
Returns: - C(N, N) np.ndarray
The square matrix of correlation coefficients. The element
![C[i,j]=C[j,i]](../_images/math/709f60b89db15874f0deced9152a19286b30d59d.png) is the Pearson’s correlation coefficient between
binned_sts[i] and binned_sts[j]. If binned_sts contains only one
neo.SpikeTrain, C=1.0.
is the Pearson’s correlation coefficient between
binned_sts[i] and binned_sts[j]. If binned_sts contains only one
neo.SpikeTrain, C=1.0.
Raises: - MemoryError
When using fast=True and binned_sts shape is large.
Warns: - UserWarning
If at least one row in binned_sts is empty (has no spikes).
See also
Notes
- The spike trains in the binned structure are assumed to cover the complete time span [t_start, t_stop) of binned_sts.
- Using fast=True might lead to MemoryError. If it’s the case, switch to fast=False.
Examples
Generate two Poisson spike trains
>>> import neo >>> from quantities import s, Hz, ms >>> from elephant.spike_train_generation import homogeneous_poisson_process >>> from elephant.conversion import BinnedSpikeTrain >>> st1 = homogeneous_poisson_process( ... rate=10.0*Hz, t_start=0.0*s, t_stop=10.0*s) >>> st2 = homogeneous_poisson_process( ... rate=10.0*Hz, t_start=0.0*s, t_stop=10.0*s) >>> cc_matrix = corrcoef(BinnedSpikeTrain([st1, st2], binsize=5*ms)) >>> print(cc_matrix[0, 1]) 0.015477320222075359
-
elephant.spike_train_correlation.covariance(binned_sts, binary=False, fast=True)[source]¶ Calculate the NxN matrix of pairwise covariances between all combinations of N binned spike trains.
For each pair of spike trains
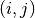 , the covariance
, the covariance ![C[i,j]](../_images/math/bf98d44b10da7feeb3ab48513f947f6939e208a9.png) is obtained by binning
is obtained by binning 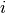 and
and 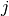 at the desired bin size. Let
at the desired bin size. Let
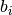 and
and  denote the binned spike trains and
denote the binned spike trains and
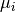 and
and 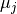 their respective averages. Then
their respective averages. Then![C[i,j] = <b_i-\mu_i, b_j-\mu_j> / (L-1)](../_images/math/f4c667d64eaf41a4ea1d13db063306e6e397aa13.png)
where <., .> is the scalar product of two vectors, and
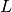 is the
number of bins.
is the
number of bins.For an input of N spike trains, an N x N matrix is returned containing the covariances for each combination of input spike trains.
If binary is True, the binned spike trains are clipped to 0 or 1 before computing the covariance, so that the binned vectors
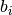 and
and
 are binary.
are binary.Parameters: - binned_sts(N, ) elephant.conversion.BinnedSpikeTrain
A binned spike train containing the spike trains to be evaluated.
- binarybool, optional
If True, the spikes of a particular spike train falling in the same bin are counted as 1, resulting in binary binned vectors
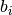 . If
False, the binned vectors
. If
False, the binned vectors 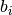 contain the spike counts per bin.
Default: False.
contain the spike counts per bin.
Default: False.- fastbool, optional
If fast=True and the sparsity of binned_sts is > 0.1, use np.cov(). Otherwise, use memory efficient implementation. See Notes [2]. Default: True.
Returns: - C(N, N) np.ndarray
The square matrix of covariances. The element
![C[i,j]=C[j,i]](../_images/math/709f60b89db15874f0deced9152a19286b30d59d.png) is
the covariance between binned_sts[i] and binned_sts[j].
is
the covariance between binned_sts[i] and binned_sts[j].
Raises: - MemoryError
When using fast=True and binned_sts shape is large.
Warns: - UserWarning
If at least one row in binned_sts is empty (has no spikes).
See also
corrcoef- Pearson correlation coefficient
Notes
- The spike trains in the binned structure are assumed to cover the complete time span [t_start, t_stop) of binned_sts.
- Using fast=True might lead to MemoryError. If it’s the case, switch to fast=False.
Examples
Generate two Poisson spike trains
>>> import neo >>> from quantities import s, Hz, ms >>> from elephant.spike_train_generation import homogeneous_poisson_process >>> from elephant.conversion import BinnedSpikeTrain >>> st1 = homogeneous_poisson_process( ... rate=10.0*Hz, t_start=0.0*s, t_stop=10.0*s) >>> st2 = homogeneous_poisson_process( ... rate=10.0*Hz, t_start=0.0*s, t_stop=10.0*s) >>> cov_matrix = covariance(BinnedSpikeTrain([st1, st2], binsize=5*ms)) >>> print(cov_matrix[0, 1]) -0.001668334167083546
-
elephant.spike_train_correlation.cross_correlation_histogram(binned_st1, binned_st2, window='full', border_correction=False, binary=False, kernel=None, method='speed', cross_corr_coef=False)[source]¶ Computes the cross-correlation histogram (CCH) between two binned spike trains binned_st1 and binned_st2.
Parameters: - binned_st1, binned_st2elephant.conversion.BinnedSpikeTrain
Binned spike trains of lengths N and M to cross-correlate. The input spike trains can have any t_start and t_stop.
- window{‘valid’, ‘full’} or list of int, optional
- ‘full’: This returns the cross-correlation at each point of overlap,
with an output shape of (N+M-1,). At the end-points of the cross-correlogram, the signals do not overlap completely, and boundary effects may be seen.
- ‘valid’: Mode valid returns output of length max(M, N) - min(M, N) + 1.
The cross-correlation product is only given for points where the signals overlap completely. Values outside the signal boundary have no effect.
- List of integers (min_lag, max_lag):
The entries of window are two integers representing the left and right extremes (expressed as number of bins) where the cross-correlation is computed.
Default: ‘full’.
- border_correctionbool, optional
whether to correct for the border effect. If True, the value of the CCH at bin
 (for
(for 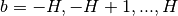 , where
, where 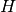 is
the CCH half-length) is multiplied by the correction factor:
is
the CCH half-length) is multiplied by the correction factor: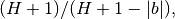
which linearly corrects for loss of bins at the edges. Default: False.
- binarybool, optional
If True, spikes falling in the same bin are counted as a single spike; otherwise they are counted as different spikes. Default: False.
- kernelnp.ndarray or None, optional
A one dimensional array containing a smoothing kernel applied to the resulting CCH. The length N of the kernel indicates the smoothing window. The smoothing window cannot be larger than the maximum lag of the CCH. The kernel is normalized to unit area before being applied to the resulting CCH. Popular choices for the kernel are
- normalized boxcar kernel: numpy.ones(N)
- hamming: numpy.hamming(N)
- hanning: numpy.hanning(N)
- bartlett: numpy.bartlett(N)
If None, the CCH is not smoothed. Default: None.
- method{‘speed’, ‘memory’}, optional
Defines the algorithm to use. “speed” uses numpy.correlate to calculate the correlation between two binned spike trains using a non-sparse data representation. Due to various optimizations, it is the fastest realization. In contrast, the option “memory” uses an own implementation to calculate the correlation based on sparse matrices, which is more memory efficient but slower than the “speed” option. Default: “speed”.
- cross_corr_coefbool, optional
If True, a normalization is applied to the CCH to obtain the cross-correlation coefficient function ranging from -1 to 1 according to Equation (5.10) in [1]. See Notes. Default: False.
Returns: - cch_resultneo.AnalogSignal
Containing the cross-correlation histogram between binned_st1 and binned_st2.
Offset bins correspond to correlations at delays equivalent to the differences between the spike times of binned_st1 and those of binned_st2: an entry at positive lag corresponds to a spike in binned_st2 following a spike in binned_st1 bins to the right, and an entry at negative lag corresponds to a spike in binned_st1 following a spike in binned_st2.
To illustrate this definition, consider two spike trains with the same t_start and t_stop: binned_st1 (‘reference neuron’) : 0 0 0 0 1 0 0 0 0 0 0 binned_st2 (‘target neuron’) : 0 0 0 0 0 0 0 1 0 0 0 Here, the CCH will have an entry of 1 at lag=+3.
Consistent with the definition of neo.AnalogSignals, the time axis represents the left bin borders of each histogram bin. For example, the time axis might be: np.array([-2.5 -1.5 -0.5 0.5 1.5]) * ms
- lagsnp.ndarray
Contains the IDs of the individual histogram bins, where the central bin has ID 0, bins to the left have negative IDs and bins to the right have positive IDs, e.g.,: np.array([-3, -2, -1, 0, 1, 2, 3])
Notes
- The Eq. (5.10) in [1] is valid for binned spike trains with at most one spike per bin. For a general case, refer to the implementation of _covariance_sparse().
- Alias: cch
References
[1] (1, 2) “Analysis of parallel spike trains”, 2010, Gruen & Rotter, Vol 7. Examples
Plot the cross-correlation histogram between two Poisson spike trains
>>> import elephant >>> import matplotlib.pyplot as plt >>> import quantities as pq
>>> binned_st1 = elephant.conversion.BinnedSpikeTrain( ... elephant.spike_train_generation.homogeneous_poisson_process( ... 10. * pq.Hz, t_start=0 * pq.ms, t_stop=5000 * pq.ms), ... binsize=5. * pq.ms) >>> binned_st2 = elephant.conversion.BinnedSpikeTrain( ... elephant.spike_train_generation.homogeneous_poisson_process( ... 10. * pq.Hz, t_start=0 * pq.ms, t_stop=5000 * pq.ms), ... binsize=5. * pq.ms)
>>> cc_hist = ... elephant.spike_train_correlation.cross_correlation_histogram( ... binned_st1, binned_st2, window=[-30,30], ... border_correction=False, ... binary=False, kernel=None, method='memory')
>>> plt.bar(left=cc_hist[0].times.magnitude, ... height=cc_hist[0][:, 0].magnitude, ... width=cc_hist[0].sampling_period.magnitude) >>> plt.xlabel('time (' + str(cc_hist[0].times.units) + ')') >>> plt.ylabel('cross-correlation histogram') >>> plt.axis('tight') >>> plt.show()
-
elephant.spike_train_correlation.spike_time_tiling_coefficient(spiketrain_1, spiketrain_2, dt=array(0.005) * s)[source]¶ Calculates the Spike Time Tiling Coefficient (STTC) as described in [1] following their implementation in C. The STTC is a pairwise measure of correlation between spike trains. It has been proposed as a replacement for the correlation index as it presents several advantages (e.g. it’s not confounded by firing rate, appropriately distinguishes lack of correlation from anti-correlation, periods of silence don’t add to the correlation and it’s sensitive to firing patterns).
The STTC is calculated as follows:
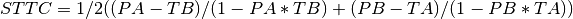
Where PA is the proportion of spikes from train 1 that lie within [-dt, +dt] of any spike of train 2 divided by the total number of spikes in train 1, PB is the same proportion for the spikes in train 2; TA is the proportion of total recording time within [-dt, +dt] of any spike in train 1, TB is the same proportion for train 2. For
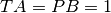 the resulting
the resulting  is replaced with
is replaced with 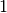 ,
since every spike from the train with
,
since every spike from the train with 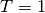 is within
[-dt, +dt] of a spike of the other train.
is within
[-dt, +dt] of a spike of the other train.This is a Python implementation compatible with the elephant library of the original code by C. Cutts written in C and avaiable at: (https://github.com/CCutts/Detecting_pairwise_correlations_in_spike_trains/blob/master/spike_time_tiling_coefficient.c)
Parameters: - spiketrain_1, spiketrain_2: neo.SpikeTrain
Spike trains to cross-correlate. They must have the same t_start and t_stop.
- dt: pq.Quantity.
The synchronicity window is used for both: the quantification of the proportion of total recording time that lies [-dt, +dt] of each spike in each train and the proportion of spikes in spiketrain_1 that lies [-dt, +dt] of any spike in spiketrain_2. Default : 0.005 * pq.s
Returns: - index: float or np.nan
The spike time tiling coefficient (STTC). Returns np.nan if any spike train is empty.
Notes
Alias: sttc
References
[1] Cutts, C. S., & Eglen, S. J. (2014). Detecting Pairwise Correlations in Spike Trains: An Objective Comparison of Methods and Application to the Study of Retinal Waves. Journal of Neuroscience, 34(43), 14288–14303.
-
elephant.spike_train_correlation.spike_train_timescale(binned_st, tau_max)[source]¶ Calculates the auto-correlation time of a binned spike train. Uses the definition of the auto-correlation time proposed in [[1], Eq. (6)]:
![\tau_\mathrm{corr} = \int_{-\tau_\mathrm{max}}^{\tau_\mathrm{max}}\
\left[ \frac{\hat{C}(\tau)}{\hat{C}(0)} \right]^2 d\tau](../_images/math/9bff1cfa7af84b7349d9e2e78c9396935d10789d.png)
where
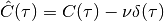 denotes
the auto-correlation function excluding the Dirac delta at zero timelag.
denotes
the auto-correlation function excluding the Dirac delta at zero timelag.Parameters: - binned_stelephant.conversion.BinnedSpikeTrain
A binned spike train containing the spike train to be evaluated.
- tau_maxpq.Quantity
Maximal integration time of the auto-correlation function.
Returns: - timescalepq.Quantity
The auto-correlation time of the binned spiketrain.
Notes
 is a critical parameter: numerical estimates
of the auto-correlation functions are inherently noisy. Due to the
square in the definition above, this noise is integrated. Thus, it is
necessary to introduce a cutoff for the numerical integration - this
cutoff should be neither smaller than the true auto-correlation time
nor much bigger.
is a critical parameter: numerical estimates
of the auto-correlation functions are inherently noisy. Due to the
square in the definition above, this noise is integrated. Thus, it is
necessary to introduce a cutoff for the numerical integration - this
cutoff should be neither smaller than the true auto-correlation time
nor much bigger.- The bin size of binned_st is another critical parameter as it defines
the discretization of the integral
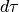 . If it is too big, the
numerical approximation of the integral is inaccurate.
. If it is too big, the
numerical approximation of the integral is inaccurate.
References
[1] Wieland, S., Bernardi, D., Schwalger, T., & Lindner, B. (2015). Slow fluctuations in recurrent networks of spiking neurons. Physical Review E, 92(4), 040901.
