elephant.spike_train_correlation.spike_train_timescale¶
-
elephant.spike_train_correlation.spike_train_timescale(binned_spiketrain, max_tau)[source]¶ Calculates the auto-correlation time of a binned spike train. Uses the definition of the auto-correlation time proposed in [[1], Eq. (6)]:
![\tau_\mathrm{corr} = \int_{-\tau_\mathrm{max}}^{\tau_\mathrm{max}}\
\left[ \frac{\hat{C}(\tau)}{\hat{C}(0)} \right]^2 d\tau](../../../_images/math/9bff1cfa7af84b7349d9e2e78c9396935d10789d.png)
where
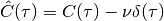 denotes
the auto-correlation function excluding the Dirac delta at zero timelag.
denotes
the auto-correlation function excluding the Dirac delta at zero timelag.Parameters: - binned_spiketrainelephant.conversion.BinnedSpikeTrain
A binned spike train containing the spike train to be evaluated.
- max_taupq.Quantity
Maximal integration time
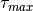 of the auto-correlation
function. It needs to be a multiple of the bin_size of
binned_spiketrain.
of the auto-correlation
function. It needs to be a multiple of the bin_size of
binned_spiketrain.
Returns: - timescalepq.Quantity
The auto-correlation time of the binned spiketrain with the same units as in the input. If binned_spiketrain has less than 2 spikes, a warning is raised and np.nan is returned.
Notes
 is a critical parameter: numerical estimates
of the auto-correlation functions are inherently noisy. Due to the
square in the definition above, this noise is integrated. Thus, it is
necessary to introduce a cutoff for the numerical integration - this
cutoff should be neither smaller than the true auto-correlation time
nor much bigger.
is a critical parameter: numerical estimates
of the auto-correlation functions are inherently noisy. Due to the
square in the definition above, this noise is integrated. Thus, it is
necessary to introduce a cutoff for the numerical integration - this
cutoff should be neither smaller than the true auto-correlation time
nor much bigger.- The bin size of binned_spiketrain is another critical parameter as it
defines the discretization of the integral
 . If it is too
big, the numerical approximation of the integral is inaccurate.
. If it is too
big, the numerical approximation of the integral is inaccurate.
References
[1] Wieland, S., Bernardi, D., Schwalger, T., & Lindner, B. (2015). Slow fluctuations in recurrent networks of spiking neurons. Physical Review E, 92(4), 040901.
